Persamaan Logaritma
Persamaan logaritma merupakan persamaan logaritma yang mengandung unsur fungsi tertentu. Persamaan ini mengandung beberapa bentuk diantaranya:
- Bentuk

Dengan bentuk seperti itu, maka persamaan dapat diubah bentuknya menjadi  . Dengan syarat a > 0 dan a ≠ 1. Sebagai contoh,
. Dengan syarat a > 0 dan a ≠ 1. Sebagai contoh,  , maka:
, maka:

Dari persamaan kuadrat tersebut dapat diketahui akar-akarnya sebagai penyelesaian:

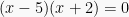
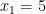 dan
dan  Dari persamaan kuadrat tersebut dapat diketahui akar-akarnya sebagai penyelesaian:
Dari persamaan kuadrat tersebut dapat diketahui akar-akarnya sebagai penyelesaian:

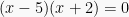
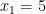 dan
dan 
- Bentuk
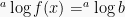
Dengan bentuk seperti itu, maka persamaan dapat diubah bentuknya menjadi f(x) = b dengan syarat a > 0, a ≠ 1 dan b > 0. Sebagai contoh, 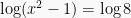 diubah bentuk menjadi:
diubah bentuk menjadi:

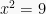
Akar-akarnya adalah:
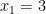 dan
dan 
- Bentuk

Dengan bentuk seperti itu, maka persamaan dapat diubah bentuknya menjadi  . Dengan syarat a > 0, a ≠ 1 dan
. Dengan syarat a > 0, a ≠ 1 dan  > 0 dan
> 0 dan  > 0. Sebagai contoh:
> 0. Sebagai contoh:
 ,
,
Menjadi:



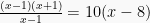
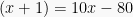

Sehingga:
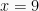
- Bentuk

Persamaan logaritma ini dapat direduksi menjadi persamaan kuadrat dengan memisalkan  . Sehingga membentuk persamaan baru:
. Sehingga membentuk persamaan baru:

Dari persamaan tersebut akan diperoleh penyelesaian fungsi y, kemudian bisa disubstitusikan kedalam  untuk mendapatkan penyelesaian fungsi x. Sebagai contoh:
untuk mendapatkan penyelesaian fungsi x. Sebagai contoh:

Misalkan 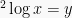 , maka persamaan barunya:
, maka persamaan barunya:


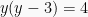
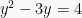


Akar-akarnya:
 dan
dan 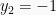
Sehingga diperoleh nilai x dari akar-akar y yaitu:



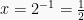
Pertidaksamaan Logaritma
Pertidaksamaan juga bisa dioperasikan pada logaritma. Pada petidaksamaan logaritma, berlaku beberapa teorema yaitu:
Saat a > 1
Saat 0 < a < 1
Sebagai contoh, menentukan nilai x yang memenuhi pertidaksamaan:
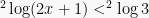
Berubah bentuk menjadi:
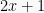
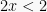

Dari pertidaksamaan tersebut diketahui bahwa a = 2, berarti a > 1. Berlaku syarat: Jika  , maka
, maka 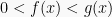 . Sehingga:
. Sehingga:



Garis bilangannya adalah:

Sama halnya dengan persamaan logaritma, pertidaksamaan logaritma sering kali dilakukan permisalan  . Permisalan ini untuk menyederhanakan dan mempermudah penyelesaiaan pertidaksamaan. Sebagai contoh penyelesaian dari:
. Permisalan ini untuk menyederhanakan dan mempermudah penyelesaiaan pertidaksamaan. Sebagai contoh penyelesaian dari:

Diubah menjadi:


Dimisalkan y = log x, maka pertidaksamaan menjadi:

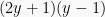
Akar-akarnya adalah :
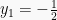 dan
dan 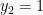
Maka nilai x adalah:
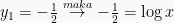



Berlaku syarat x > 0, dan x ≠ 1, maka garis bilangannya adalah:

Penyelesaiannya adalah:
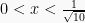 atau
atau 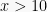
Pertidaksamaan Harga Mutlak Logaritma
Operasi logaritma bisa dilakukan dalam sebuah harga mutlak. Penyelesaiannya mengikuti sifat-sifat harga mutlak dan logaritma. Harga mutlak tersebut memiliki sifat-sifat:
- Jika
 dengan
dengan  > 0, maka
> 0, maka  < x <
< x < 
- Jika
 dengan
dengan  > 0, maka x <
> 0, maka x <  atau x >
atau x > 
Penyelesaian pertidaksamaan logaritma dalam harga mutlak ini dapat dikerjakan seperti contoh:
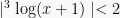
Berdasarkan sifat  , maka:
, maka:

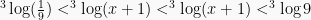
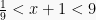

Berdasarkan sifat  , maka:
, maka:

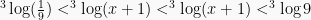
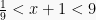

Contoh Soal Persamaan dan Pertidaksamaan Logaritma dan Pembahasan
Contoh Soal 1: Persamaan Logaritma
Tentukan penyelesaian dari  (UMPTN ’92)
(UMPTN ’92)
Pembahasan 1:


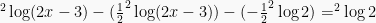


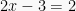

Contoh Soal 2: Persamaan Logaritma
Tentukan nilai x dari persamaan 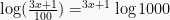 (UMPTN ’93)
(UMPTN ’93)
Pembahasan 2:
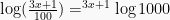
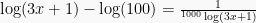
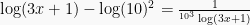
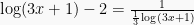
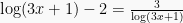
Misalkan 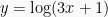 , maka persamaannya:
, maka persamaannya:

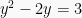

Berdasarkan sifat  , maka:
, maka:

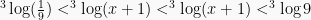
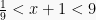

Contoh Soal Persamaan dan Pertidaksamaan Logaritma dan Pembahasan
Contoh Soal 1: Persamaan Logaritma
Tentukan penyelesaian dari  (UMPTN ’92)
(UMPTN ’92)
Pembahasan 1:


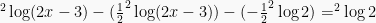


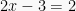

Contoh Soal 2: Persamaan Logaritma
Tentukan nilai x dari persamaan 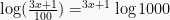 (UMPTN ’93)
(UMPTN ’93)
Pembahasan 2:
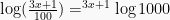
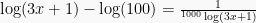
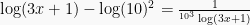
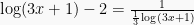
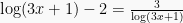
Misalkan 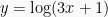 , maka persamaannya:
, maka persamaannya:

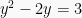

Berdasarkan sifat  , maka:
, maka:

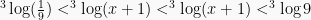
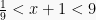

Contoh Soal Persamaan dan Pertidaksamaan Logaritma dan Pembahasan
Contoh Soal 1: Persamaan Logaritma
Tentukan penyelesaian dari  (UMPTN ’92)
(UMPTN ’92)
Pembahasan 1:


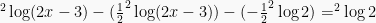


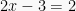

Contoh Soal 2: Persamaan Logaritma
Tentukan nilai x dari persamaan 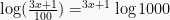 (UMPTN ’93)
(UMPTN ’93)
Pembahasan 2:
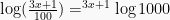
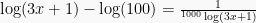
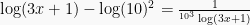
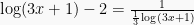
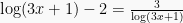
Misalkan 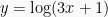 , maka persamaannya:
, maka persamaannya:

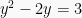

Berdasarkan sifat  , maka:
, maka:

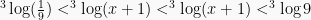
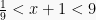

Contoh Soal Persamaan dan Pertidaksamaan Logaritma dan Pembahasan
Contoh Soal 1: Persamaan Logaritma
Tentukan penyelesaian dari  (UMPTN ’92)
(UMPTN ’92)
Pembahasan 1:


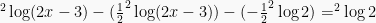


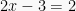

Contoh Soal 2: Persamaan Logaritma
Tentukan nilai x dari persamaan 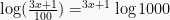 (UMPTN ’93)
(UMPTN ’93)
Pembahasan 2:
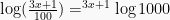
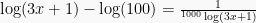
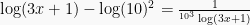
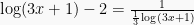
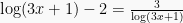
Misalkan 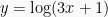 , maka persamaannya:
, maka persamaannya:

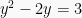

Berdasarkan sifat  , maka:
, maka:

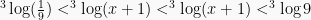
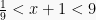

Contoh Soal Persamaan dan Pertidaksamaan Logaritma dan Pembahasan
Contoh Soal 1: Persamaan Logaritma
Tentukan penyelesaian dari  (UMPTN ’92)
(UMPTN ’92)
Pembahasan 1:


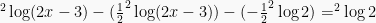


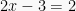

Contoh Soal 2: Persamaan Logaritma
Tentukan nilai x dari persamaan 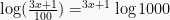 (UMPTN ’93)
(UMPTN ’93)
Pembahasan 2:
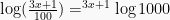
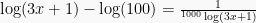
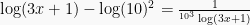
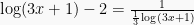
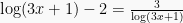
Misalkan 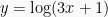 , maka persamaannya:
, maka persamaannya:

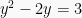

Berdasarkan sifat  , maka:
, maka:

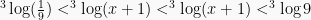
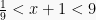

Contoh Soal Persamaan dan Pertidaksamaan Logaritma dan Pembahasan
Contoh Soal 1: Persamaan Logaritma
Tentukan penyelesaian dari  (UMPTN ’92)
(UMPTN ’92)
Pembahasan 1:


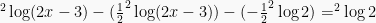


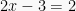

Contoh Soal 2: Persamaan Logaritma
Tentukan nilai x dari persamaan 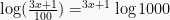 (UMPTN ’93)
(UMPTN ’93)
Pembahasan 2:
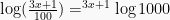
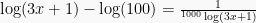
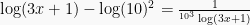
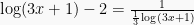
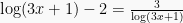
Misalkan 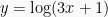 , maka persamaannya:
, maka persamaannya:

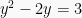

(UMPTN ’92)
(UMPTN ’93)
, maka persamaannya:
,namun
tidak bisa jadi penyelesaian karena bernilai negatif.
adalah (UMPTN ’96)
dan
. Sehingga intervalnya:


