VEKTOR MATEMATIKA – PENGERTIAN, RUMUS, DAN CONTOH SOAL

vektor adalah ruas garis berarah yang memiliki besaran (nilai) dan arah tertentu. Secara geometris, suatu vektor dapat digambarkan sebagai ruas garis berarah dengan panjang ruas garis menyatakan besar vektor dan arah ruas garis menyatakan arah vektor.

Sebuah vektor dapat dinotasikan dengan beberapa ketentuan, diantaranya:

Definisi dari vektor sendiri adalah ruas garis berarah. Maka, bentuk dari vektor bisa kamu lihat pada gambar vektor berikut ini.

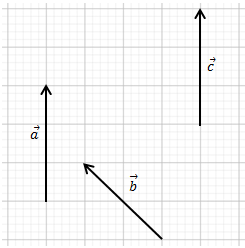
Nah, setelah kalian amati gambar vektor di atas, 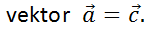. Kedua vektor tersebut mempunyai panjang vektor dan arah yang sama meskipun letaknya berbeda.

Jenis-Jenis Vektor Matematika

Vektor ternyata terbagi menjadi beberapa jenis, yaitu:

1. Vektor Nol : Suatu vektor yang panjangnya nol dan tidak memiliki arah vektor yang jelas.

2. Vektor Posisi : Suatu vektor yang posisi titik awalnya di O (0,0), sedangkan posisi titik ujungnya di satu titik tertentu (selain titik O).

3. Vektor Satuan : Suatu vektor yang panjangnya satu satuan.

4. Vektor Basis : Suatu vektor yang panjangnya satu satuan, tapi arahnya searah dengan sumbu koordinat.

Vektor Pada Bidang (R2)

Kita lanjut, yuk! Karena vektor merupakan salah satu bagian dari geometri, berarti vektor dapat digambarkan pada sebuah bidang (R2) atau sebuah ruang (R3). Kalau vektor berada pada bidang, maka akan dinyatakan dalam dua sumbu koordinat, yaitu sumbu-x dan sumbu-y. Sedangkan vektor yang berada pada ruang (R3), akan dinyatakan dalam tiga sumbu koordinat, yaitu sumbu-x, sumbu-y, dan sumbu-z.

Panjang Vektor pada Bidang

Sesuai dengan pengertiannya, vektor memiliki panjang tertentu. Nah, untuk menentukan panjang suatu vektor pada bidang (R2), kamu bisa menggunakan rumus berikut.

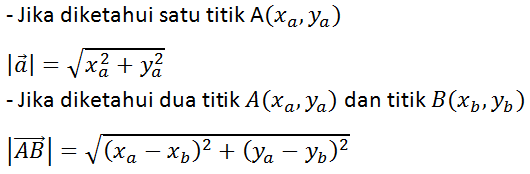
Operasi Vektor pada Bidang

Operasi pada vektor tidak jauh berbeda dengan operasi aljabar kok, Sobat. Operasi vektor pada bidang meliputi: penjumlahan, pengurangan, perkalian vektor dengan skalar, dan perkalian dua vektor.

Penjumlahan Vektor

Dalam penjumlahan dua vektor, secara geometri, terdapat dua macam cara penjumlahan yang bisa digunakan, yaitu: cara segitiga dan cara jajar genjang.

• Penjumlahan dua vektor dengan cara segitiga:

• Penjumlahan dua vektor dengan cara jajar genjang:

Namun, secara aljabar, penjumlahan vektor hanya menjumlahkan koordinat titik pusat vektor dengan titik ujungnya.

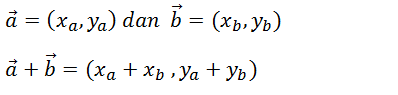
2. Pengurangan Vektor
Pengurangan dua vektor pada dasarnya sama dengan penjumlahan kedua vektor. Namun, secara geometri, yang membedakan adalah terdapat salah satu vektor yang memiliki arah berlawanan sehingga bernilai negatif. Sedangkan secara aljabar, hanya mengurangi titik-titik pada koordinat vektornya.

3. Perkalian Vektor dengan Skalar
Perkalian antara vektor dengan skalar adalah hasil kali suatu bilangan skalar k dengan sebuah vektor a.